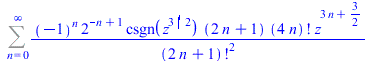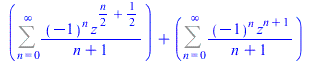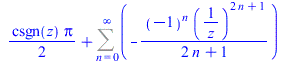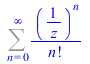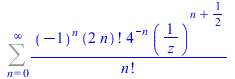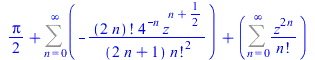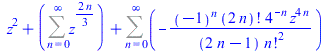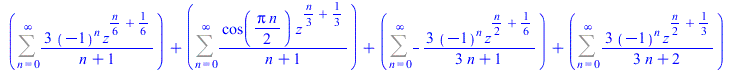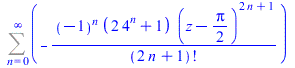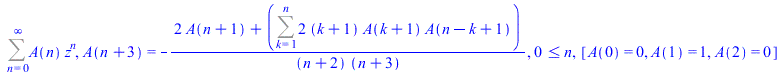Symbolic Computation of Formal Power Series in Maple
February 2021
This worksheet demonstrates some capacities of a new package FPS (Formal Power Series) that can be used to recover power series formulas and sometimes discover unexpected ones. The package implements symbolic algorithms from
- Teguia Tabuguia, Bertrand and Koepf, Wolfram. Symbolic computation of hypergeometric type and non-holonomic
power series. arXiv preprint arXiv:2102.04157. 2021 (submitted)
- Teguia Tabuguia, Bertrand. Power Series Representations of Hypergeometric Type and Non-Holonomic Functions in Computer Algebra. Ph.D. thesis, University of Kassel, Germany. https://kobra.uni-kassel.de/handle/123456789/11598. May 2020.
- Teguia Tabuguia, Bertrand. A variant of van Hoeij's algorithm to compute hypergeometric term solutions of holonomic recurrence equations. arXiv preprint arXiv:2012.11513. 2021 (submitted)
![[FPS, FindQRE, FindRE, HolonomicDE, LinearDE, QDE, Taylor, dispSet, mfoldHyper, rectohyperterm, sumhyperRE]](images/FormalPowerSeriesMaple_1.gif) |
(1) |
1. Overview of the method
Consider for example f(z):=arctan(z)+cos(z). First, the code computes a differential equation of a special type, called
holonomic, satisfied by f(z). This is done in the following way.
![Typesetting:-mprintslash([f := `+`(arctan(z), cos(z))], [`+`(arctan(z), cos(z))])](images/FormalPowerSeriesMaple_2.gif) |
(2) |
| > |
DE:=HolonomicDE(f,F(z)) |
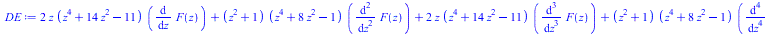
 |
(3) |
Second, the differential equation is converted into a recurrence equation. This is done internally by FindRE which computes the recurrence equation directly.
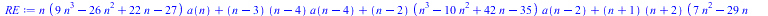
 |
(4) |
Then the coefficient of the power series sought is computed as (m-fold hypergeometric term) solutions of the obtained recurrence equation. The algorithm used is new.
![[[2, {`/`(`*`(`^`(-1, n)), `*`(n)), `/`(`*`(`^`(-1, n)), `*`(factorial(`+`(`*`(2, `*`(n))))))}]]](images/FormalPowerSeriesMaple_7.gif) |
(5) |
These are the coefficients of the even part of the expansion (there are only 2-fold hypergeometric term solutions over the rationals). For the odd part, mfoldHyper can be used as follows.
| > |
mfoldHyper(RE,a(n),ml=[2,1]) |
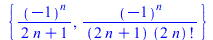 |
(6) |
Finally a linear combination of the involved power series is sought with verification of the initial values, and we get
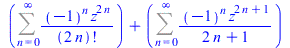 |
(7) |
At the current time, this complete approach for hypergeometric type power series is new for all computer algebra systems. The same computations can be done for series with negative and even fractional powers.
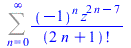 |
(8) |
| > |
FPS(cos(sqrt(z))+sin(z^(1/3)),z,n); |
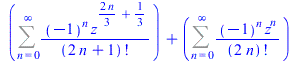 |
(9) |
If the given input is not of hypergeometric type but holonomic, then a recursive formula is given for its representation. On the other hand, there is another approach used which mainly deals with expressions that are not holonomic like tan(z), log(1+sin(z)), (1+tan(z))/(1-tan(z)), etc., by computing quadratic differential equations. We find it a little inconvenient to introduce Bernoulli or Euler numbers in formulas since it could not give full information to the user. Instead we return recursive formulas that the user can use to recover truncated series.
![Typesetting:-mprintslash([f := ln(`+`(1, sin(z)))], [ln(`+`(1, sin(z)))])](images/FormalPowerSeriesMaple_12.gif) |
(10) |
![Typesetting:-mprintslash([DE := `+`(`*`(diff(F(z), `$`(z, 2)), `*`(diff(F(z), z))), diff(F(z), `$`(z, 3))) = 0], [`+`(`*`(diff(diff(F(z), z), z), `*`(diff(F(z), z))), diff(diff(diff(F(z), z), z), z)) ...](images/FormalPowerSeriesMaple_13.gif) |
(11) |
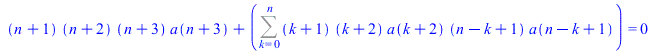 |
(12) |
| > |
FPS(f,z,n,fpstype=Quadratic) |
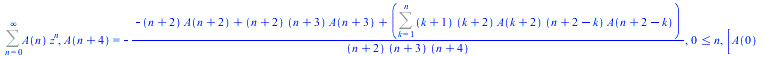
 |
(13) |
| > |
FPS((1+tan(z))/(1-tan(z)),z,n,fpstype=Quadratic) |
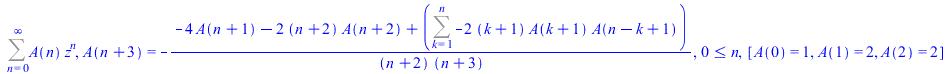 |
(14) |
| > |
FPS(tan(z),z,n,fpstype=Quadratic) |
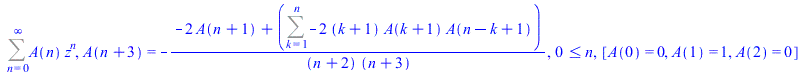 |
(15) |
| > |
FPS(1/(exp(z)-1),z,n,fpstype=Quadratic) |
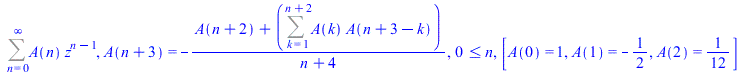 |
(16) |
1. Provided commands
The reader should be able to guess the meaning of symbols used in the syntaxes below.
- FPS(f,z,n,z0): z0 being optional, to compute the power series formula of f in the indeterminate z. By default z0=0, and hypergeometric type series are sought by default. A forth argument fpstype=Holonomic or fpstype=Quadratic can be specified to give the output as a recursive formula deduced from a holonomic recurrence equation, or as a recursive formula deduced from a non-linear recurrence equation (deduced from a quadradic differential equation), respectively. The maximum order of the holonomic differential equation internally computed can be increased by supplying the argument maxdeorder=N, where N>=10.
- mfoldHyper(RE,a(n)): to find m-fold hypergeometric term solutions of holonomic recurrence equations, for every positive integer m. A third argument C (mfoldHyper(RE,a(n),C)) can be specified for computations involving algebraic numbers (Complex numbers, irrational numbers, parameters).
- rectohyperterm(RE,a(n)): A particular case of mfoldHyper corresponding to the case m=1. This is equivalent to LREtools[hypergeomsols].
- sumhyperRE(L,a(n)): to compute a holonomic recurrence equation satisfied by a given list of hypergeometric terms.
- dispSet(P1,P2,x,F): to compute the dispersion set of the polynomials P1:=P1(x) and P2:=P2(x). By default, the computations are done over the field of coefficients. Extension fields can be supplied as a set F of algebraic numbers.
- HolonomicDE(f,F(z)): to compute a holonomic differential equation satisfied by a given expression f:=f(z). A third argument, a positive integer greater than 10, may be specified as the maximum order of the differential equation sought. For special functions, the argument "SpecialFunctions" must be supplied.
- QDE(f,F(z)): to compute a quadratic differential equation satisfied by a given expression.
- FindRE(f,z,a(n)): to compute a holonomic recurrence equation satisfied by a given expression.
- FindQRE(f,z,a(n)): to compute a non-holonomic recurrence equation (from QDE) satisfied by a given expression.
- Taylor(f,z,z0,N): to compute truncated taylor expansions of holonomic functions. This is usefull sometimes since it is faster for computing larger-order Taylor expansions.
- LinearDE(f,F(z)): to compute a linear differential equation with coefficients that are not necessarily polynomials.
3. Classical examples
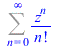 |
(17) |
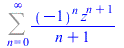 |
(18) |
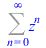 |
(19) |
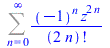 |
(20) |
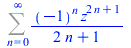 |
(21) |
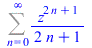 |
(22) |
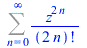 |
(23) |
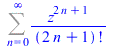 |
(24) |
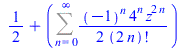 |
(25) |
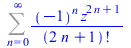 |
(26) |
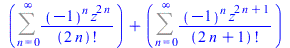 |
(27) |
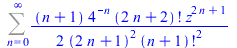 |
(28) |
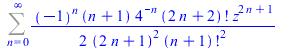 |
(29) |
![Sum(`/`(`*`(`(p)`[n], `*`(`^`(z, n))), `*`(factorial(n))), n = 0 .. infinity)](images/FormalPowerSeriesMaple_33.gif) |
(30) |
4. More thoughtfull series
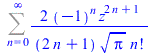 |
(31) |
| > |
FPS(arcsin(z)^2/z^2,z,n) |
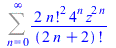 |
(32) |
| > |
FPS(exp(arcsinh(z)),z,n) |
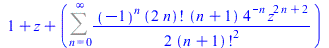 |
(33) |
| > |
FPS(exp(arcsin(z)),z,n) |
![`+`(Sum(`/`(`*`((`+`(`-`(`*`(`/`(1, 2), `*`(I)))))[n], `*`((`*`(`/`(1, 2), `*`(I)))[n], `*`(`^`(4, n), `*`(`^`(z, `+`(`*`(2, `*`(n)))))))), `*`(factorial(`+`(`*`(2, `*`(n)))))), n = 0 .. infinity), Su...](images/FormalPowerSeriesMaple_37.gif) |
(34) |
| > |
FPS(sqrt((1-sqrt(1-z))/z),z,n) |
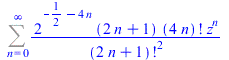 |
(35) |
| > |
FPS((z+sqrt(1+z^2))^alpha,z,n) |
![`+`(Sum(`/`(`*`(`^`(-1, n), `*`((`+`(`-`(`*`(`/`(1, 2), `*`(alpha)))))[n], `*`((`+`(`*`(`/`(1, 2), `*`(alpha))))[n], `*`(`^`(4, n), `*`(`^`(z, `+`(`*`(2, `*`(n))))))))), `*`(factorial(`+`(`*`(2, `*`(n...](images/FormalPowerSeriesMaple_39.gif) |
(36) |
| > |
FPS(exp(z)-2*exp(-z/2)*cos(sqrt(3)*z/2+Pi/3),z,n) |
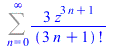 |
(37) |
| > |
FPS(1/2*ln((1+z)/(1-z))-arctan(z),z,n) |
![Sum(`+`(`/`(`*`(`/`(2, 3), `*`((`/`(3, 4))[n], `*`(`^`(z, `+`(`*`(4, `*`(n)), 3))))), `*`((`/`(7, 4))[n]))), n = 0 .. infinity)](images/FormalPowerSeriesMaple_41.gif) |
(38) |
| > |
FPS(ln(1+z+z^2+z^3),z,n) |
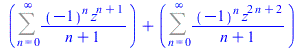 |
(39) |
| > |
FPS(cos(4*arccos(z)),z,n) |
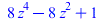 |
(40) |
| > |
FPS(arcsin(z)+arccos(z),z,n) |
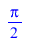 |
(41) |
| > |
FPS(arctan((z+t)/(1-z*t)),z,n) |
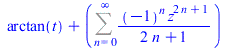 |
(42) |
| > |
FPS(arctan((z+t)/(1-z*t))-arctan(z),z,n) |
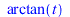 |
(43) |
| > |
FPS(sin(3*arccos(z))/sqrt(1-z^2),z,n) |
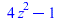 |
(44) |
| > |
FPS(1/(sqrt(1-4*z))*((1-sqrt(1-4*z))/2*z)^2,z,n) |
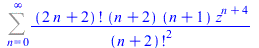 |
(45) |
| > |
FPS(sqrt(sqrt(8*z^3+1)-1),z,n) |
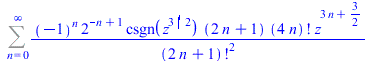 |
(46) |
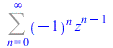 |
(47) |
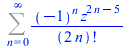 |
(48) |
| > |
FPS(ln(1+z)+cos(z),z,n) |
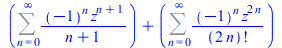 |
(49) |
| > |
FPS(cos(z)+z*sin(z),z,n) |
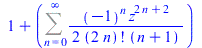 |
(50) |
| > |
FPS(sin(z)+z*cos(z),z,n) |
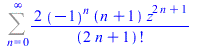 |
(51) |
| > |
FPS(ln(1+sqrt(z)+z+z^(3/2)),z,n) |
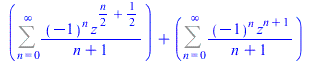 |
(52) |
| > |
FPS(arctan(z)+exp(z^2),z,n) |
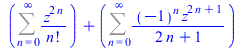 |
(53) |
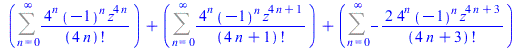 |
(54) |
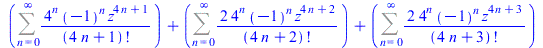 |
(55) |
| > |
FPS((cos(z)+sin(z))^2,z,n) |
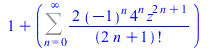 |
(56) |
| > |
FPS((cos(z)+sin(z))^3,z,n) |
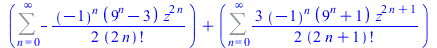 |
(57) |
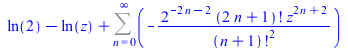 |
(58) |
| > |
FPS(exp(z)+ln(1+z),z,n,1) |
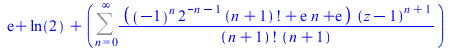 |
(59) |
| > |
FPS(sin(z)+exp(z),z,n,Pi) |
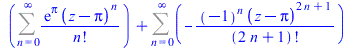 |
(60) |
| > |
FPS(arctan(z),z,n,infinity) |
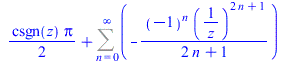 |
(61) |
| > |
FPS(exp(1/z),z,n,infinity) |
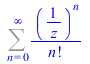 |
(62) |
| > |
FPS(sqrt(Pi)*exp(z)*(1-erf(sqrt(z))),z,n,infinity) |
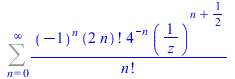 |
(63) |
| > |
FPS(arctan(z)^2,z,n,fpstype=Holonomic) |
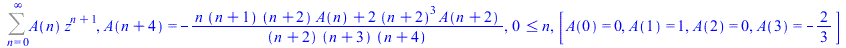 |
(64) |
| > |
FPS(log(1+z)^2,z,n,fpstype=Holonomic) |
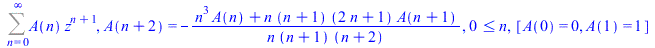 |
(65) |
| > |
FPS(arccos(z^(1/2))+exp(z^2),z,n) |
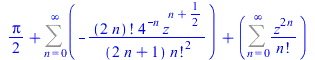 |
(66) |
| > |
FPS(exp(arcsinh(z^2))+1/(1-z^(2/3)),z,n) |
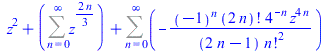 |
(67) |
| > |
FPS(z*ln(z)^2+arcsin(z),z,n) |
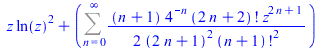 |
(68) |
| > |
FPS(ln(1+sqrt(z))+arctan(z^(1/3)),z,n) |
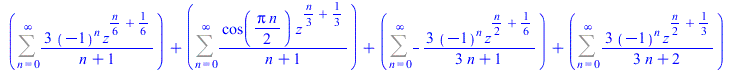 |
(69) |
| > |
FPS(sin(2*z)+cos(z),z,n,Pi/2) |
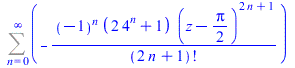 |
(70) |
| > |
FPS(tanh(z),z,n,fpstype=Quadratic) |
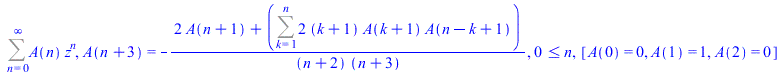 |
(71) |
| > |
FPS(exp(z)*log(1+z),z,n,fpstype=Holonomic) |
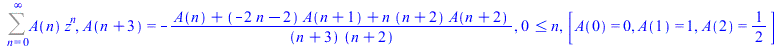 |
(72) |
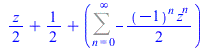 |
(73) |
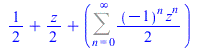 |
(74) |
![Sum(`*`(`+`(`/`(`*`(`*`(`/`(1, 2), `*`(I)), `*`(`^`(-1, n), `*`((`+`(1, `-`(I)))[n]))), `*`(`+`(`-`(n), I), `*`(factorial(n)))), `/`(`*`(`*`(`/`(1, 2), `*`(I)), `*`(`^`(-1, n), `*`((`+`(1, I))[n]))), ...](images/FormalPowerSeriesMaple_78.gif) |
(75) |
![Sum(`*`(`+`(`/`(`*`(`/`(1, 2), `*`(`^`(-1, `+`(n, 1)), `*`((`+`(1, `-`(I)))[`+`(n, 1)]))), `*`(`+`(`-`(n), `+`(`-`(1), I)), `*`(factorial(`+`(n, 1))))), `-`(`/`(`*`(`/`(1, 2), `*`(`^`(-1, `+`(n, 1)), ...](images/FormalPowerSeriesMaple_79.gif) |
(76) |
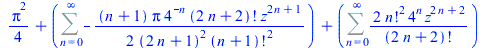 |
(77) |
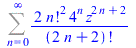 |
(78) |
| > |
FPS(arccos(z)^2-arcsin(z)^2,z,n) |
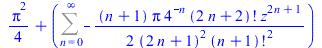 |
(79) |
| > |
FPS(sin(z)+sinh(z),z,n) |
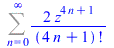 |
(80) |
| > |
FPS(cos(2*z)+sin(3*z),z,n) |
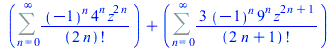 |
(81) |
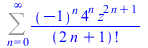 |
(82) |
| > |
FPS(sinh(z)*sin(z),z,n) |
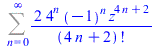 |
(83) |
| > |
FPS(cosh(z)*cos(z),z,n) |
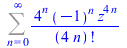 |
(84) |
| > |
FPS(exp(z)*cosh(z),z,n) |
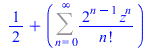 |
(85) |
| > |
FPS(arctanh(z)+sqrt(1+z)+1/sqrt(1+z),z,n) |
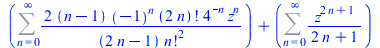 |
(86) |
| > |
FPS(sinh(z)^2+cosh(z)^2,z,n) |
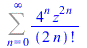 |
(87) |
| > |
FPS(-cosh(z)^2+sinh(z)^2,z,n) |
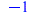 |
(88) |
| > |
FPS(1/(p-z^2)/(q-z^3),z,n) |
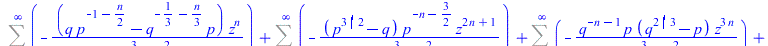 |
(89) |
| > |
FPS(2*arctanh(sin(2*z)/(1+cos(2*z))),z,n,fpstype=Quadratic) |
| > |
FPS(ln((1+tan(z))/(1-tan(z)))-2*arctanh(sin(2*z)/(1+cos(2*z))),z,n,fpstype=Quadratic) |
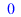 |
(91) |
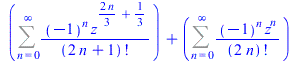
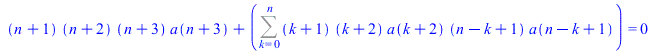
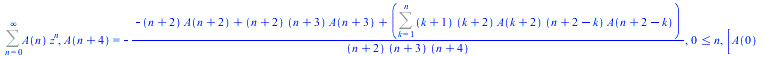
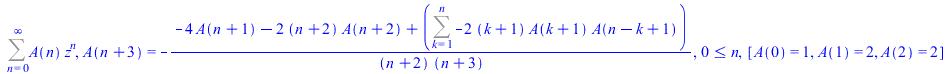
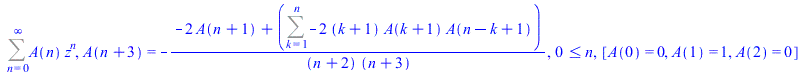
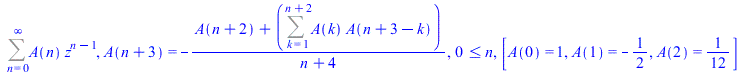
![`+`(Sum(`/`(`*`((`+`(`-`(`*`(`/`(1, 2), `*`(I)))))[n], `*`((`*`(`/`(1, 2), `*`(I)))[n], `*`(`^`(4, n), `*`(`^`(z, `+`(`*`(2, `*`(n)))))))), `*`(factorial(`+`(`*`(2, `*`(n)))))), n = 0 .. infinity), Su...](images/FormalPowerSeriesMaple_37.gif)
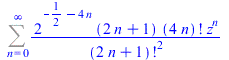
![`+`(Sum(`/`(`*`(`^`(-1, n), `*`((`+`(`-`(`*`(`/`(1, 2), `*`(alpha)))))[n], `*`((`+`(`*`(`/`(1, 2), `*`(alpha))))[n], `*`(`^`(4, n), `*`(`^`(z, `+`(`*`(2, `*`(n))))))))), `*`(factorial(`+`(`*`(2, `*`(n...](images/FormalPowerSeriesMaple_39.gif)
![Sum(`+`(`/`(`*`(`/`(2, 3), `*`((`/`(3, 4))[n], `*`(`^`(z, `+`(`*`(4, `*`(n)), 3))))), `*`((`/`(7, 4))[n]))), n = 0 .. infinity)](images/FormalPowerSeriesMaple_41.gif)