Zurück
Zusatz zu Projektaufgabe 1:
Bestimmen Sie zu dem zweiten Text den Koinzidenzindex, sowie die Größe
wobei
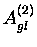 die Anzahl der Paare gleicher Buchstaben
aus verschiedenen Spalten des Vigenère-Tableaus und
die Anzahl der Paare gleicher Buchstaben
aus verschiedenen Spalten des Vigenère-Tableaus und
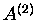 die Anzahl aller möglichen Buchstabenpaare
mit Buchstaben aus verschiedenen Spalten des Vigenère-Tableaus bezeichne.
die Anzahl aller möglichen Buchstabenpaare
mit Buchstaben aus verschiedenen Spalten des Vigenère-Tableaus bezeichne.
Modifizieren Sie anschließend den Friedman-Test, indem Sie
a)
diese Größe
b) den Koinzidenzindex
(und nicht 1/26) für die näherungsweise Berechnung der Schlüssellänge benutzen.
Projektaufgabe 2
1.Teil: Fingerübungen
1) Lösen Sie die folgenden Kongruenzen:
2) Bestimmen Sie die Lösungsmenge
3) Ermitteln Sie die folgenden Werte der Eulerschen
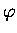 -Funktion :
-Funktion :
2.Teil: Warmwerden mit RSA
Dechiffrieren Sie die folgende Nachricht, die RSA-verschlüsselt an jemanden gesendet wurde, nennen wir ihn Bob, der den öffentlichen Schlüssel 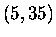 besitzt:
Chiffrieren Sie die erhaltene verschlüsselte Nachricht nochmals mit dem öffentlichen Schlüssel von Bob und senden Sie sie an Bob.
Übersetzen Sie die Nachricht, mit
besitzt:
Chiffrieren Sie die erhaltene verschlüsselte Nachricht nochmals mit dem öffentlichen Schlüssel von Bob und senden Sie sie an Bob.
Übersetzen Sie die Nachricht, mit
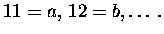
Warum ist Bob´s Schlüssel nicht geeignet?
Angenommen, jemand anders, nennen wir sie Catherine, habe den öffentlichen Schlüssel 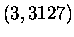 . Was senden Sie an Bob, um ihm vorzugaukeln, die Nachricht stamme von ihr? Glauben Sie, dass Bob darauf hereinfällt?
. Was senden Sie an Bob, um ihm vorzugaukeln, die Nachricht stamme von ihr? Glauben Sie, dass Bob darauf hereinfällt?
3.Teil: (Keine!?) Angst vor großen Zahlen
Es seien folgende öffentliche Schlüssel vergeben:
Gruppe A:
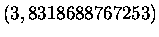
Gruppe B:
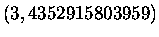
Gruppe C:
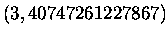
Gruppe D:
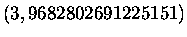
Aufgabe : Jede Gruppe X verschlüssele eine Nachricht, die nur aus einem Buchstaben besteht und sende sie an die Gruppe 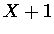 (mod
(mod 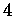 ).
Was müssen Sie beachten?
).
Was müssen Sie beachten?
Diskutieren Sie die folgende Situation:
A schlägt Gruppe B ein geheimes Treffen vor.
Das gleiche tun Gruppe C und D.
Ausserdem versuchen die Gruppen, das Treffen der jeweils anderen zu verhindern.
Die Gruppen kommunizieren über ein öffentliches nicht abhörsicheres Netz.
Zurück
Projektwoche
2000-01-14
![]()
![]()
![]()
![]()
![]() (mod
(mod ![]() ).
Was müssen Sie beachten?
).
Was müssen Sie beachten?