
Alois und Dietmar beim Nachdenken. Jeder Punkt zeigt eine der “dick-köpfigen” Stecknadeln.
Zwei weitere Fotos mit den damaligen Ergebnissen:
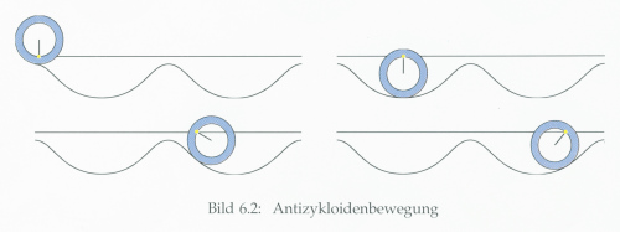
Antizykloiden
Mathematik als sozialer Prozess –
und wie sich Technologie weiterentwickelt
nebst einem Ausblick auf Roads and Wheels.
Ralf Schaper
1984 Klagenfurt: Wie bei früheren Tagungen zur Visualisierung in der
Mathematik an der Universität trafen sich Einige am Vorabend, dem
Sonntag dem 15. Juli, beim “Wadler” in der Villacher Straße. Damals war
es ein schönes österreichisches Lokal mit Biergarten unter Kastanien.
Wie üblich lernte man sich schon kennen und sprach beim Essen über
Arbeitsgruppen und Themen für die kommende Tagung. Heute kann ich es ja
offen formulieren: Nicht nur einige Themen passten mir nicht, sondern
auch, wer die zugehörigen AGs leiten sollte. Also: Was tun? Nun, der
Abend wurde länger, das Essen mundete und der Grüne Veltliner regte an.
Und
so entstand im Gespräch mit Bernd Bornscheuer und Dietmar Hennig die
Idee: Wir “drehen ’mal ’ne Beobachtung um”: Beobachtet man z.B. einen
Reflektor in den Speichen eines Fahrrades und die Bahn dieses
Reflektors, wenn das Rad auf einer geraden Straße abrollt, so erhält man
als Bahn Zykloiden. Das sind bekannte Kurven, die beispielsweise auch bei der Beschreibung des ptolemäischen Weltbildes bei den Planetenbahnen eine Rolle spielen, also seit Jahrhunderten wohlbekannt.
Nun im übertragenen Sinne unsere “Schnapsidee”; der Zustand der sog. Weinseligkeit war allerdings nicht erreicht:
Der frei gewählte Punkt im Rad soll sich auf einer Geraden bewegen!
Wie “krumm” muss dazu die “Straße” sein und wie sehen diese Straßen aus?
Das ist – wie wir später lernten – ein sog. inverses Problem: Gegeben ist ein Ziel, ein Resultat, wie kann es erreicht werden?
Die oben Genannten bildeten zusammen mit Alois Vilim aus Wien dann in
der folgenden Woche eine AG. Die zu ergründenden Kurven nannten wir
Antizykloiden.
Zitat aus dem Tagungsband [1, S. 174]:
Während
des Workshops stand uns keine Literatur bzgl. Antizykloiden und
derartiger inverser Probleme bei Kurven zur Verfügung. Die Kürze des
Workshops ließ eine Simulation des Problems auf einem Rechner nicht zu.
Wir entschieden uns daher dafür, mit Pappe, Zwirn, Stecknadeln und einer
Pinwand reale Modelle zu erstellen.
Auf einer Pappscheibe von ca. 6
cm Durchmesser konstruierten wir ein reguläres 64-Eck. Eine Reißzwecke
fixierte den Gleitpunkt P. Die aus der Pappscheibe herausragende Spitze
der Reißzwecke wurde durch zwei festgespannte Zwirnsfäden auf der
"Geraden" geführt und so mit Hilfe des 64-Ecks eine Approximation einer
Antizykloide konstruiert. Wir fixierten dann die Kurve mit
"dick-köpfigen" Stecknadeln und konnten auf ihnen die Pappscheibe
abrollen lassen. Die hier gezeigten Bilder sind Fotografien der so
erstellten Kurven für 3 Lagen des Gleitpunktes P .
Soweit der Tagungsband.

Alois und Dietmar
beim Nachdenken. Jeder Punkt zeigt eine der “dick-köpfigen” Stecknadeln.
Zwei weitere Fotos mit den damaligen Ergebnissen:


Nun zwei Bilder aus dem Tagungsband [4], später erzeugt mit viel mehr Stecknadeln:
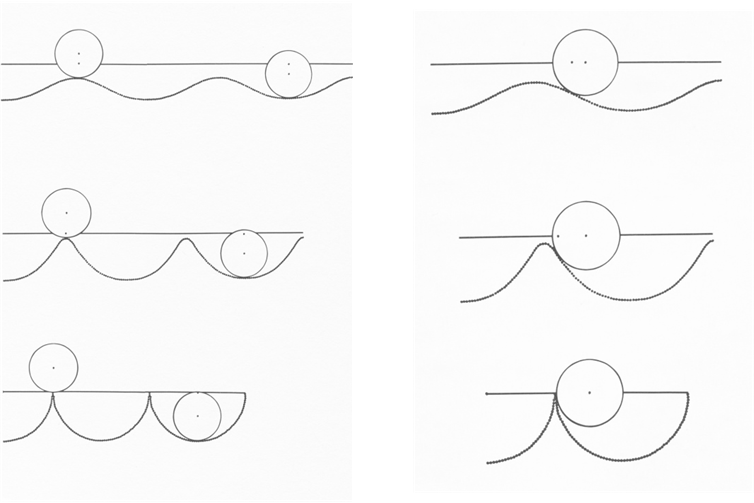
Die
Maxima der Antizykloiden werden angenommen, wenn der Mittelpunkt des
“Rades” genau über dem Berührpunkt auf der “Straße” liegt. Analoges gilt
für die Minima.
Wendepunkte werde angenommen, wenn Mittelpunkt und Berührpunkt beide auf der “Leit”-Geraden liegen.
Hans Dirnböck, der uns auf vielen Tagungen zur Visualisierung in der Mathematik nicht nur durch seine komplexen technischen Zeichnungen und seine vielfältigen Kenntnisse aus der Geometrie faszinierte, war vom Thema der Antizykloiden so begeistert, dass er es ausweitete und darüber in Klagenfurt promovierte: “Die Antizykloidenbewegung. Die Kreisrollung mit einer gegebenen geraden Bahn” erschien dann 1987 [2]. Er stellte das Problem in einen größeren kinematischen Zusammenhang, erörterte die didaktischen Möglichkeiten und fertigte damals mit BASIC-Programmen sogar Daumenkinos an, um die Bewegung auf einer Antizykloide zu visualisieren. Er zeigte, dass Antizykloiden nicht nur bei rollenden Kreisen entstehen sondern insbesondere auch bei der Spur der Brennpunkte rollender Ellipsen auf Geraden.

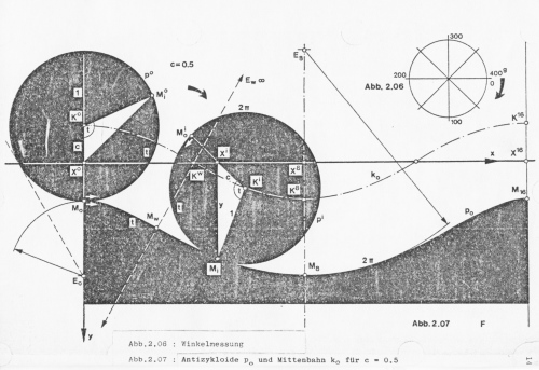
Daraus einige Reproduktionen. Zuerst Seite 14 zur Herleitung einer Parametrisierung einer Antizykloide beim rollenden Kreis.
Seite 83: Die elliptische Kettenlinie als Antizykloide.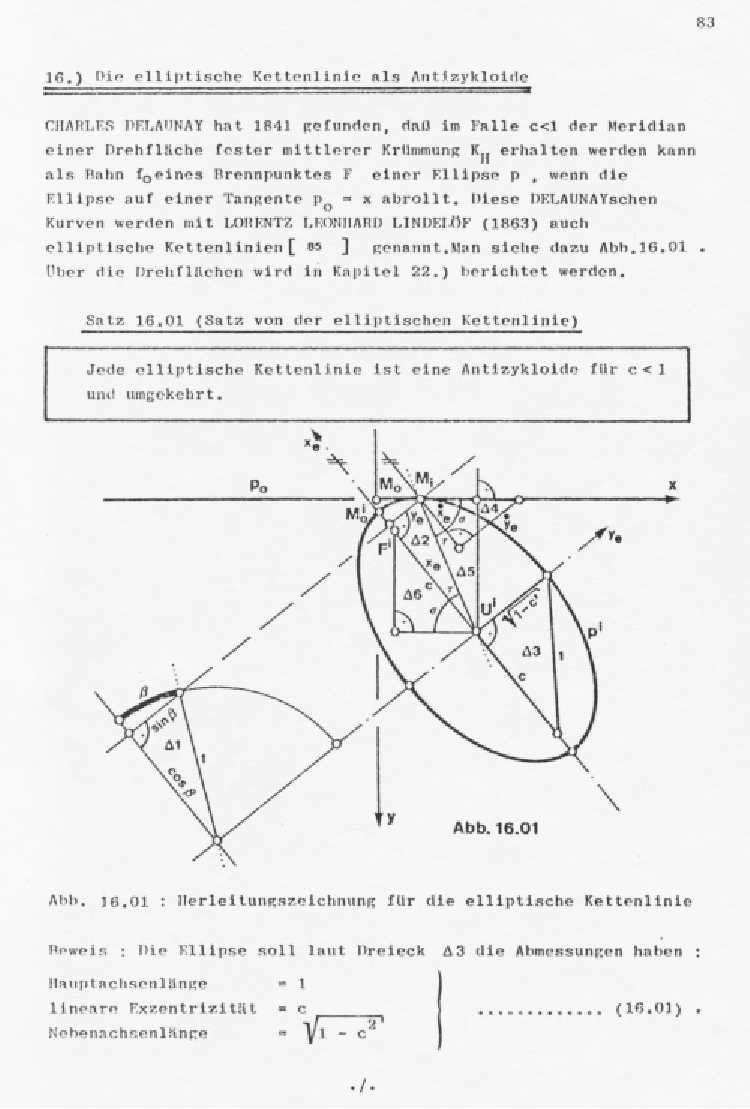
Seite 274: Mit einem Sharp PC-1251 mit Drucker/Kassetteneinheit wurden u.a. auch die Daumenkinos
für Antizykloiden mit Hilfe von BASIC-Programmen erzeugt. Das war ca. 1985!
Ein Problem ist dabei die numerische Auswertung des Integrals
![]()
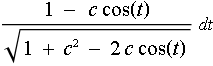 .
.
Dazu
weiter unten noch einige überraschende Beobachtungen.
Zwei Daumenkinos: Breite jeweils 4,5 cm.

Die Vorlagen dafür:
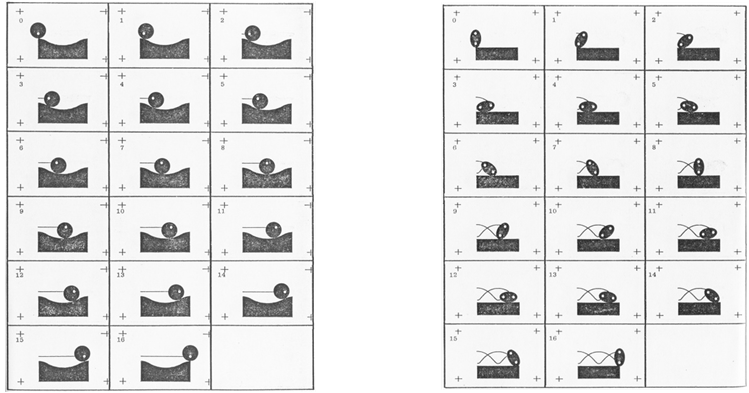
Beim Scrollen dieses Textes kann jetzt der Effekt des Daumenkinos wahrgenommen werden; altes Medium in neuer Technologie!
1994 gab es dann in meinem Buch “Grafik mit Mathematica”
[6, S. 182] u.a.dieses Bild:
Das eben erwähnte Integral ![]()
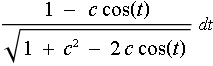 konnte damals mit Mathematica, Version 2.2, für feste Werte c numerisch ausgewertet werden:
konnte damals mit Mathematica, Version 2.2, für feste Werte c numerisch ausgewertet werden:
![]()
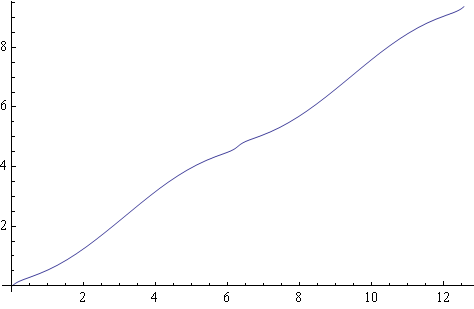
Das ergibt dann etwa dieses Bild für die entsprechende Antizykloide:
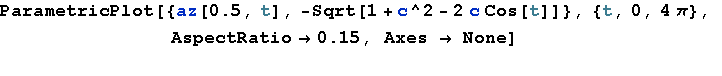

Die Rechenzeit lag 1994 im Bereich von Minuten. So können einzelne Grafiken erzeugt werden, aber keine interaktiven Animationen!
2010 erhielt ich von Wolfram Research die Chance, eine Prereleaseversion von Mathematica zu testen. Mit Version 8.0.0.2 konnte nun das Integral
![]()
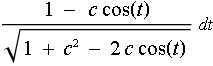
explizit als Summe zweier elliptischer Integrale dargestellt werden:
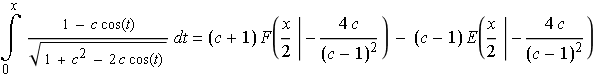 ,
,
wobei jeweils F(x|γ) ein elliptisches Integral erster Art und E(x|γ) ein elliptisches Integral zweiter Art ist.
Die Rechenzeit zum Finden dieser Darstellung betrug auf meinen vier Jahre alten Laptop ca. 73 Sekunden:

![]()
Eine Überraschung kam mit Version 8.0.0.3: Die Rechenzeit betrug nun ca. 343 Sekunden, also fast das fünffache!

![]()
Version 8.0.0.4 brachte dann wieder eine Verbesserung auf ca. 92 Sekunden:
Mit Mathematica, Version 7,
habe ich die Rechnung nach vier Stunden ohne Ergebnis abgebrochen. Doch
nun bestand die Chance mit Version 7 mit der Darstellung als Summe der
zwei elliptischen Integralen weiter zu arbeiten.
Bei den rollenden Ellipsen sind dann noch weitere, ähnliche Integrale zu lösen, u.a.:
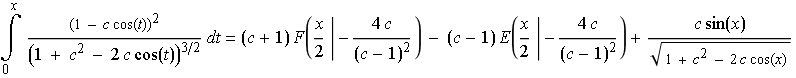 .
.
Das dauerte dann mit Version 8.0.0.4 über
3,5 Minuten:
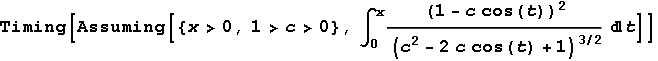
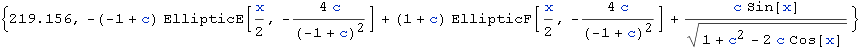
Ende September 2010 – beim Schreiben dieses Textes – erlebte ich
noch eine große Überraschung: Ich probierte die Integrale zu lösen bei http://integrals.wolfram.com, also beim “Wolfram Mathematica Online Integrator: The world’s only full-power integration solver”. Die Eingabe von
![]()
im Integrator lieferte schon nach kurzer Zeit (Time to compute: 5.65 second) in InputForm folgendes Ergebnis
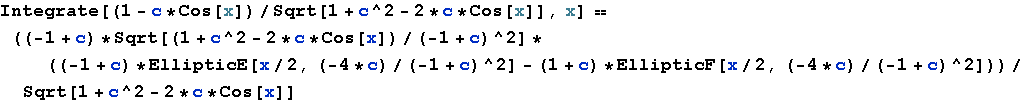
Dies Ergebnis sieht erst einmal viel komplizierter aus als das oben gefundene in InputForm:

TraditionalForm ermöglicht dann leicht einen Vergleich und beruhigt. Mit etwas Überlegung erkennt man die Gleichheit.

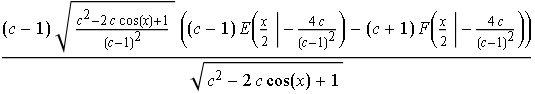
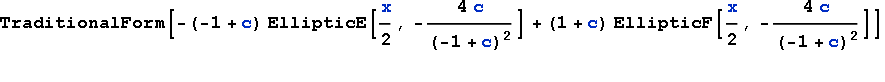
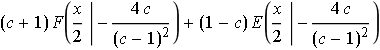

Wolfram Research stellt im Netz mit WolframAlpha eine – wie sie es nennen –
knowledge engine, also eine neuartige Suchmaschine, zur Verfügung.
Die Eingabe von
Integrate[ (1 - c Cos[t])/Sqrt[1 + c^2 - 2 c Cos[t]], {t, 0, x}]
lieferte bei den ersten Versuchen die Antwort
Computation timed out. Experimental feature: Try again with more time »
Später war das Antwortverhalten unterschiedlich: Try again lieferte manchmal kein Ergebnis und manchmal innerhalb einer sehr ausführlichen Darstellung auch
Alternate form of the integral assuming c and x are positive:
![]()
Mitte September wurden die beiden folgenden “Apps” im Wolfram Demonstrations Project freigeschaltet:
Anticycloid Curves I: A Rolling Circle
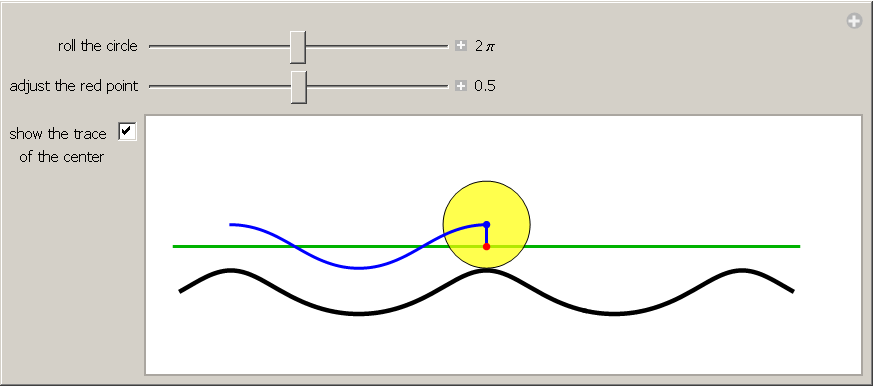
Bei diesem Beispiel läßt sich schön erkennen, wann zwei Kurven “parallel” erscheinen.
Anticycloid Curves II: A Rolling Ellipse
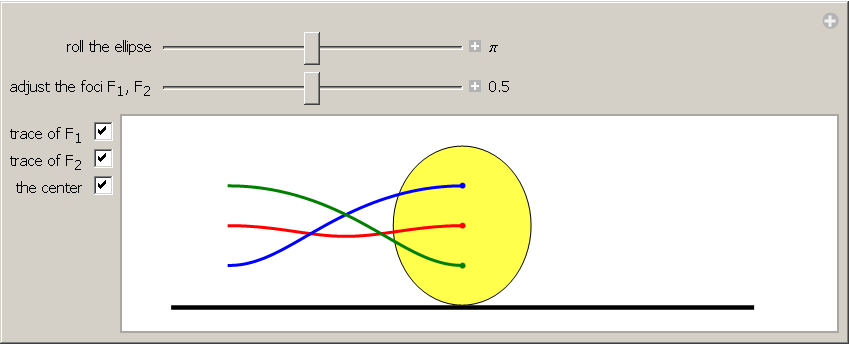
Die Programme können als .nbp bzw. die Quelltexte als .nb
Dateien geladen werden; siehe weiter unten.
Roads and Wheels
“Nicht”-MathematikerInnen
mag die oben beschriebene Situation zur Entstehung der mathematischen
Fragestellung der Antizykloiden befremden und in der Meinung bestärken: Die spinnen, die Mathematiker!
Diesem Vorurteil kann begegnet werden durch die Beobachtung, dass
Mathematik auch eine Geisteswissenschaft ist, in der das Denken frei ist
und oft einfach formulierbare Fragen zu schwierigen mathematischen
Problemen führen können. Dazu jetzt die ähnliche Fragestellung: Kann
ein Fahrrad mit quadratischen Rädern gebaut werden und wie sieht dann
eine Straße aus, auf der damit bequem gefahren werden kann?
Die spinnen, die Mathematiker !!!
Gemach: Die Lösung hat es bis in das Deutsche Museum in München geschafft und ist mittlerweile selbst bei YouTube mehrfach zu betrachten. Dazu die Einzelheiten:
Angeregt durch ein Exponat im Exploratorium in San Francisco hat Stan Wagon 1992
[3] mit Leon Hall die Theorie dazu gelegt und dann 1997 – wie Andere vor ihm – ein Dreirad
gebaut, auf
dem bequem zu fahren ist.

Ein Bild sagt mehr als tausend Worte
wird oft fälschlich als ein altes chinesisches Sprichwort zitiert.
Trotzdem: Ein Video bzw. eine Animation überzeugen noch mehr als tausend
Worte, selbst wenn der Vorspann ca. 40 Sekunden dauert und es bei YouTube liegt. Dort gibt es
u.a. zwei weitere einschlägige Videos: Math Midway square-wheeled tricycle bzw. Square-wheeled bike on a catenary curve in 3D Studio.
Im Deutschen Museum wird das Prinzip nur an einem vierrädrigen Modell demonstriert.
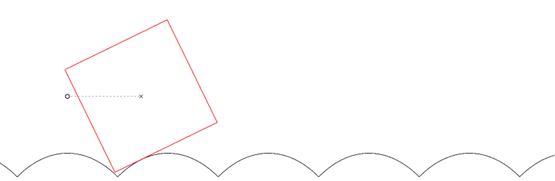
Jetzt noch ein weiterer Link zu YouTube. Dort wird am Ende des Videos auch das Prinzip erläutert, wie in dem folgenden Einzelbild, das aus einer guten Animation stammt, von den englischen WIKIPEDIA-Seiten.
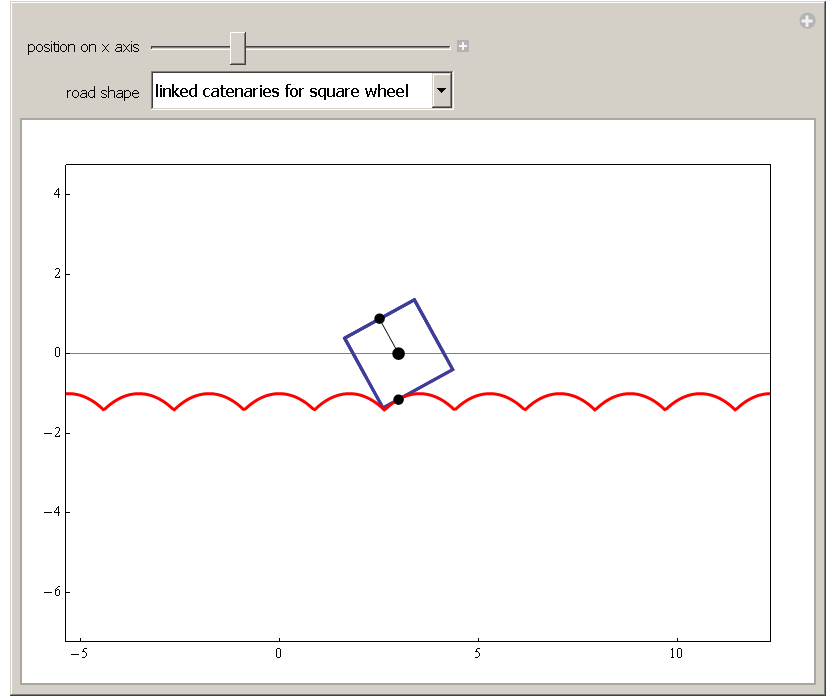
Stan Wagon hat beim Wolfram Demonstrations Project sein “app” Roads and Wheels
eingestellt. Darin beläßt er es nicht bei quadratischen Rädern,
dreieckige rollen auch. Unter anderem wird dort auch die Radform für
eine sägezahnförmige Straße gezeigt:
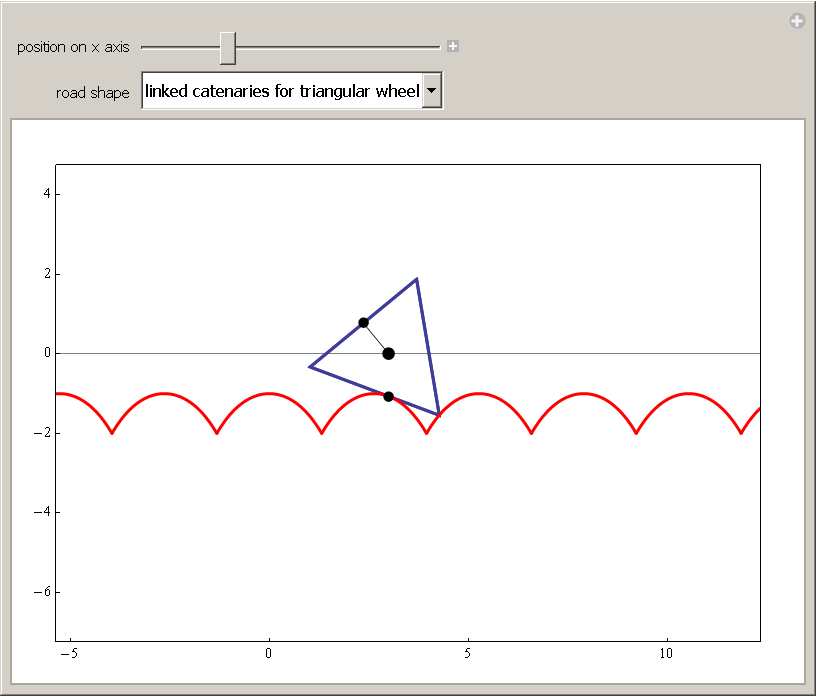
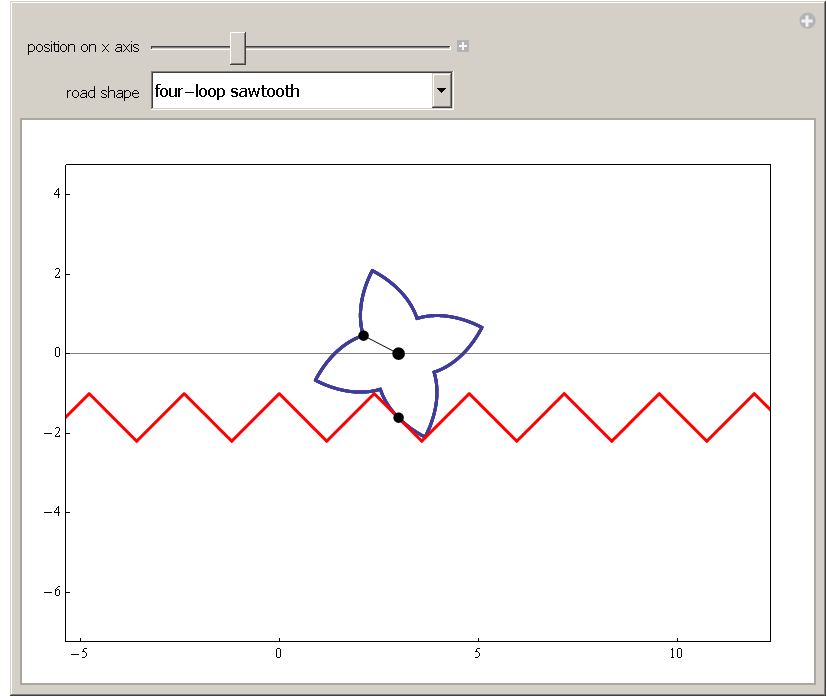
Räder in Gestalt eines regelmäßigen Dreiecks bis hin zum regelmäßigen Achteck läßt Michael Schreiber bei
Regular Polygon Rolling on a Catenary rollen.

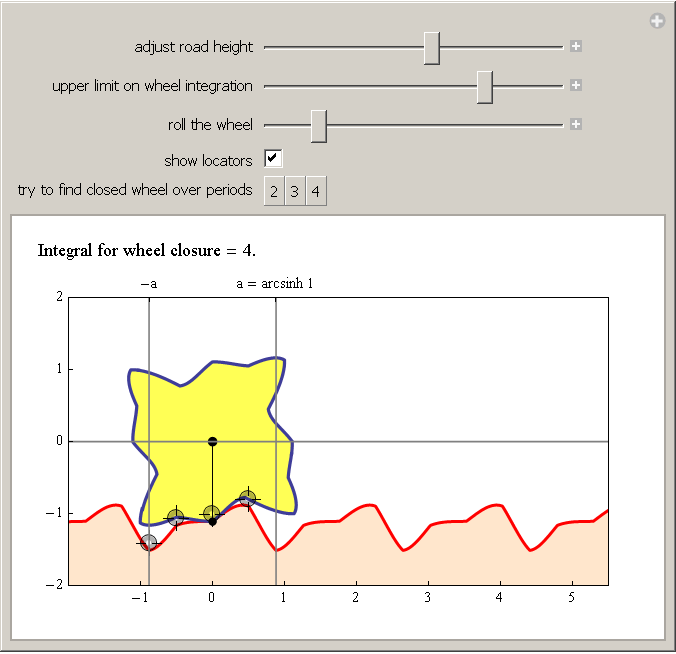
Ein Mathematiker vom Format von Stan Wagon beläßt es nicht bei solch regelmäßigen Rädern: Shaping a Road and Finding the Corresponding Wheel
behandelt vielfältige, interaktiv formbare Straßenprofile und
untersucht, ob es dazu Räder gibt. Das ist mathematisch schon sehr
anspruchsvoll.
Zum Schluss seien noch einige Hinweise [5], [7],
[8] zur mathematischen Herleitung bei quadratischen Rädern bzw. zu dem Zusammenhang mit der Kettenlinie (Catenary) angeführt.
Die erwähnten Programme können als .nbp bzw. die Quelltexte als .nb
Dateien jeweils geladen werden unter
http://demonstrations.wolfram.com/AnticycloidCurvesIARollingCircle/
http://demonstrations.wolfram.com/AnticycloidCurvesIIARollingEllipse/
http://demonstrations.wolfram.com/RoadsAndWheels/
http://demonstrations.wolfram.com/RegularPolygonRollingOnACatenary/
http://demonstrations.wolfram.com/ShapingARoadAndFindingTheCorrespondingWheel/
Zum interaktiven Betrachten dieser Programme ist entweder Mathematica nötig oder der kostenlose Mathematica-Player, der zu finden ist unter
http://www.wolfram.com/products/player/download.cgi
Ein Preview kann jeweils auch schon direkt im Netz – ohne zusätzliche Programme – angesehen werden.
[1]
Bernd Bornscheuer, Dietmar Hennig, Ralf Schaper
Antizykloiden.
In
[4], 173 – 177.
[2]
Hans Dirnböck
Die Antizykloidenbewegung. Die Kreisrollung mit einer gegebenen geraden Bahn.
Klagenfurt: Verlag Heyn, 1987.
[3]
Leon Hall, Stan Wagon
Roads and Wheels.
Mathematics Magazine, 1992 (65) 283 – 301.
[4]
Hermann Kautschitsch, Wolfgang Metzler (Hrsg.)
Anschauung und mathematische Modelle.
4. Workshop zur “Visualisierung in der Mathematik” in Klagenfurt vom 16. bis 21. Juli 1984.
Wien, Stuttgart: Hölder-Pichler-Tempsky, Teubner, 1985.
[5]
Ivars Peterson
Riding on Square Wheels.
2004
http://www.maa.org/mathland/mathtrek_04_ 05_ 04.html
[6]
Ralf Schaper
Grafik mit Mathematica. Von den Formeln zu den Formen.
Bonn: Addison-Wesley, 1994.
[7]
Stephanie Scheuer
Rolling Smoothly on a Saw-Tooth Road: The Theory for a Wheel.
http://www.snc.edu/math/images/MAASawToothRoad.pdf
[8]
Hans Walser
Das qudratische Rad.
http://www.math.unibas.ch/~walser/Miniaturen/M63_Quadratisches_Rad/Square_Wheel.pdf
Ralf Schaper
http://www.mathematik.uni-kassel.de/~rascha/