Vieweg Computeralgebra

Wolfram Koepf / Adi Ben-Israel / Robert P. Gilbert
Mathematik mit DERIVE
1993. XIV, 394 Seiten. Mit 80 Abbildungen, zahlreichen Übungsaufgaben und Mustersitzungen sowie einer Einführung in DERIVE.
Paperback, DM 49.80, ISBN 3-528-06549-4.
Das Buch ist vergriffen. Daher kann es HIER heruntergeladen werden.
Der Anhang Einführung in DERIVE kann separat heruntergeladen werden.

Dieses Buch ist ein Lehrbuch der höheren Mathematik, insbesondere der Analysis einer Variablen. Neu ist die Zuhilfenahme des symbolischen Mathematikprogramms DERIVE als technisches Hilfsmittel zur praxisnahen und dennoch strengen Wissensvermittlung. Alle dargestellten Konzepte werden durch praktische Übungen mit DERIVE unterstützt. Dabei werden sowohl die numerischen, die symbolischen als auch die graphischen Fähigkeiten solcher Systeme zum besseren Verständnis der betrachteten Konzepte herangezogen.

Inhaltsangabe
Kapitel 1: Mengen und Zahlen Mengen und Aussagen Natürliche Zahlen und vollständige Induktion Die reellen Zahlen Variablen Gleichungen und Ungleichungen Zwei fundamentale Eigenschaften der reellen Zahlen Die komplexen Zahlen Abzählbare und überabzählbare Mengen
Kapitel 2: Der Euklidische Raum Der zweidimensionale euklidische Raum Die Gaußsche Zahlenebene
Kapitel 3: Funktionen und Graphen Reelle Funktionen und ihre Graphen Lineare Funktionen und Geraden Reelle Polynome Polynominterpolation Rationale Funktionen im Reellen Rationale Funktionen im Komplexen Umkehrfunktionen und algebraische Funktionen
Kapitel 4: Folgen, Konvergenz und Grenzwerte Konvergenz reeller Zahlenfolgen Fundamentale Konvergensätze für Reihen
Kapitel 5: Die elementaren transzendenten Funktionen Potenzreihen Die Exponential-, Sinus- und Kosinusreihe Eigenschaften der Exponentialfunktion Eigenschaften der trigonometrischen Funktionen Die komplexe Exponentialfunktion Die hyperbolischen Funktionen
Kapitel 6: Stetige Funktionen Grenzwerte und Stetigkeit Einseitige Grenzwerte Fundamentale Eigenschaften stetiger Funktionen Uneigentliche Grenzwerte und Grenzwerte für 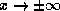Umkehrfunktionen der elementaren Funktionen
Kapitel 7: Das Riemann-Integral Riemann-Integrierbarkeit Integrale und Flächeninhalt Das unbestimmte Integral
Kapitel 8: Numerische Integration Wozu numerische Integration? Das Trapezverfahren Die Simpsonsche Formel
Kapitel 9: Differentiation Das Tangentenproblem Die Ableitung Ableitungsregeln Höhere Ableitungen Lokale Eigenschaften differenzierbarer Funktionen Die Kettenregel und implizite Differentiation
Kapitel 10: Globale Eigenschaften differenzierbarer Funktionen Der Mittelwertsatz der Differentialrechnung Globale Extremwerte und Monotonieeigenschaften Konvexität Die Regel von de l'Hospital Das Newton-Verfahren Chaos in der Analysis
Kapitel 11: Integrationstechniken Der Hauptsatz der Differential- und Integralrechnung Integration rationaler Funktionen Integration durch Substitution Partielle Integration Uneigentliche Integrale Volumen- und Oberflächenberechnungen
Kapitel 12: Gleichmäßige Konvergenz und Potenzreihen Gleichmäßige Konvergenz Potenzreihen Taylorapproximation Lagrange-Interpolation
Kapitel 13: Anhang: Einführung in DERIVE
Literaturverzeichnis Symbolverzeichnis DERIVE Stichwortverzeichnis Stichwortverzeichnis

Vorwort
Anläßlich eines Forschungsaufenthalts 1988/1989 von Bob Gilbert (University of Delaware, USA) am Fachbereich Mathematik der Freien Universität Berlin wurde ich durch ihn auf die Verwendung symbolischer Mathematikprogramme, und zwar des Computeralgebrasystems MACSYMA, in der mathematischen Forschung aufmerksam gemacht. Von diesem Zeitpunkt an kam ich von dem Gedanken der Benutzung solcher Programme in der mathematischen Lehre nicht mehr los.
Die Miniaturisierung in der Computertechnologie hatte derartige Programme nun auf kleinsten Rechnern verfügbar gemacht, und ich war sicher, daß dies die Praxis von Mathematikerinnen und Mathematikern sowie Mathematikanwendern in der nahen Zukunft radikal verändern wird. Anstatt schwierige Integrale von Hand auszurechnen - mit der Gefahr, sich in langwierigen Teilschritten zu verrechnen -, wird z. B. der zukünftige Bauingenieur versuchen, das betreffende Integral zunächst mit einem Mathematikprogramm zu lösen. Nur, wenn er hiermit scheitert, wird er zur bewährten Handberechnung übergehen. Wir wollen nicht verhehlen, daß auch dies eine nicht zu unterschätzende Gefahr birgt, nämlich die, Ergebnissen von Mathematikprogrammen unbegrenzt Vertrauen zu schenken. Genauso, wie man ein von Hand berechnetes Resultat durch Kontrollrechnungen so lange überprüfen muß, bis man sich des Ergebnisses sicher ist, muß man die Ergebnisse, die ein Mathematikprogamm erzeugt, einer sorgfältigen Überprüfung unterziehen.
Wenn aber solche Programme sowohl in der Forschung als auch in der Praxis von Bedeutung sind, sollten sie in der mathematischen Lehre ebenfalls eine Rolle spielen. Weil die Praxis der Arbeit mit einem Mathematikprogramm einer entsprechenden Schulung bedarf, muß diese in die Mathematikausbildung integriert werden. Dabei kann die Benutzung eines Mathematikprogramms in der mathematischen Lehre gleichzeitig ein großartiges Hilfsmittel sein. Wir beschlossen, gemeinsam ein Mathematik-Lehrbuch unter Verwendung eines Computeralgebrasystems zu schreiben. Zu dieser Zeit kam gerade das Mathematikprogamm DERIVE auf den Markt, und wir waren sofort sicher, daß dies das richtige Hilfsmittel für unseren Zweck darstellt.
DERIVE vereinigt graphische Fähigkeiten, die der Bearbeitung mit Papier und Bleistift gänzlich versagt bleiben, mit numerischen und symbolischen Rechenfähigkeiten, die häufig über die Möglichkeiten einer Handberechnung hinausgehen, und ist dabei kinderleicht zu bedienen. Man soll nun andererseits nicht glauben, daß Schülerinnen und Schüler bzw. Studentinnen und Studenten bei der Arbeit mit einem Mathematikprogramm gar nichts mehr selbst rechnen müssen. Ganz im Gegenteil wird man einem Mathematikprogramm oft nur dann die erhoffte Information entlocken können, wenn man über mögliche Umformungsmethoden und -mechanismen genauestens Bescheid weiß. In der Tat bedeutet der Einsatz von DERIVE für die Ausbildung, daß man sich mehr auf die zugrundeliegenden mathematischen Konzepte konzentrieren kann und sollte. Eine rein mechanische Benutzung von DERIVE ist jedenfalls nicht zu empfehlen.
Ich bekam von der Alexander von Humboldt-Stiftung ein Forschungsstipendium für einen Forschungsaufenthalt an der University of Delaware/USA zur Verfügung gestellt, wo ich zusammen mit Bob Gilbert und Adi Ben-Israel (Rutgers-University, USA) an der Einbindung von DERIVE in die Mathematikausbildung arbeitete. Ferner wurde in den Jahren 1990-1992 von der FNK (Ständige Kommission für Forschung und wissenschaftlichen Nachwuchs) der FU Berlin mein diesbezügliches Forschungsprojekt Symbolische Programmierung gefördert.
Nach meinem Forschungsaufenthalt in den Vereinigten Staaten begann ich, im Rahmen der Analysis-Vorlesungen am Fachbereich Mathematik der Freien Universität Berlin meine Erfahrungen in die Praxis umzusetzen. Aus dieser Vorlesungsaktivität ist das vorliegende Buch entstanden.
In erster Linie ist das Buch also für Mathematikstudenten an deutschen Hochschulen gedacht. Das Buch ermöglicht es, den kanonischen Stoff durchzunehmen und den Studentinnen und Studenten gleichzeitig die intelligente Benutzung von DERIVE beizubringen. Dabei wurde die Benutzung von DERIVE nicht zum Selbstzweck, sondern als didaktisches Hilfsmittel eingesetzt. Wirklich rechenintensive Problemstellungen sind dann nicht von vornherein aussichtslos.
Die folgende Vorgehensweise hat sich als günstig herausgestellt: Unsere Studentinnen und Studenten haben in der ersten Semesterwoche unter Anleitung den Anhang über DERIVE (Kapitel 13) selbständig durchgearbeitet. Dies gab ihnen genügend Kenntnisse über die Benutzung von DERIVE, um in der Folge Übungsaufgaben mit DERIVE erfolgreich bearbeiten zu können. In der Regel war eine der 5 wöchentlichen Übungsaufgaben zur expliziten Benutzung von DERIVE gedacht. Zur Behandlung der Übungsaufgaben standen unseren Studentinnen und Studenten die PCs des Computer-Labors am Fachbereich Mathematik zur Verfügung.
Die im Buch integrierten DERIVE-Sitzungen habe ich als Dozent mit DERIVE vorgeführt. Dazu genügen im Prinzip Folien mit der Bildschirminformation von DERIVE. Besser ist natürlich ein LCD-Display-Bildschirm, mit dem sich mit Hilfe eines Overheadprojektors der Computerbildschirm an die Wand werfen läßt. Mit dieser Ausrüstung können die DERIVE-Sitzungen direkt vorgeführt werden.
Im übrigen stellte sich heraus, daß nur sehr wenige Studentinnen und Studenten noch keine Berührung mit Computerprogrammen gehabt hatten und daß den meisten die Arbeit mit DERIVE leicht fiel.
Gleichzeitig mit unseren Bemühungen, die Benutzung von DERIVE oder anderen Mathematikprogrammen für den Mathematikunterricht auszuloten, wurde diese Fragestellung auch in folgenden Zusammenhängen untersucht:

• In der Zeitschrift Didaktik der Mathematik und auch in weiteren didaktikorientierten Zeitschriften wird dieses Thema seit einiger Zeit ausgiebig erörtert. Man siehe dazu z. B. die auf S. 376 zitierten Arbeiten [Engel], [Schönwald], [KB], [Scheu], [Koepf1], [Koepf2], [Koepf3], [Koepf4] und [Treiber].
• Das österreichische Unterrichtsministerium hat eine Lizenz von DERIVE für Österreichs Gymnasien erworben, s. [Kutzler].

• Gymnasiallehrerinnen und -lehrer, die in ihrem Unterricht mit DERIVE arbeiten wollen und das Buch dazu als zusätzliches Unterrichtsmaterial verwenden, werden vielfältige Anregungen für die Anwendung von DERIVE schöpfen können. Wir empfehlen die Vorstellung zum Stoff passender DERIVE-Sitzungen zusammen mit der Bearbeitung der mit dem Symbol versehenen Übungsaufgaben. Einige davon verbinden in ausgezeichneter Weise mathematische Wissensvermittlung mit dem Einsatz von DERIVE.
• Besonders interessierte Schülerinnen und Schüler der gymnasialen Oberstufe können mit Hilfe von DERIVE auch ein wenig Luft in der (noch) höheren Mathematik schnuppern, und sie werden sogleich ausgebildet in der Benutzung eines Mathematikprogramms, das vielleicht in Kürze bereits die Taschenrechner ablösen wird. Bereits jetzt gibt es DERIVE im Westentaschenformat, s. [Kutzler].
• Schließlich bietet sich das Buch für die Benutzung in der Mathematikausbildung an Fachhochschulen an. Gerade hier, wo es auf eine praxisnahe Ausbildung ankommt, kommt man an Mathematikprogrammen in der nahen Zukunft nicht vorbei.

• Primzahlen, s. Kapitel 13 sowie [Scheu].
• Definition des Integrals, s. Kapitel 7-8 sowie [KB].
• Definition von e, s. § 4.2 und § 5.2.
• Newtonverfahren, s. § 10.5 sowie [Treiber].
• Iteration und Chaos, s. § 10.6 und [Zeitler].
• Reihenkonvergenz, s. § 4.4, § 11.3, § 12.3 sowie [Koepf4].
• Lagrange-Interpolation, s. § 3.4 und § 12.4 sowie [Koepf3].
• Rekursionsformeln für Integrale durch partielle Integration, s. § 11.4.

• Für Dezimaldarstellungen verwenden wir den Dezimalpunkt statt des Dezimalkommas, zum einen, um eine mit Taschenrechner- oder Computerausgaben verträgliche Darstellung zu gewährleisten, zum anderen, um Verwechslungen bei Vektoren vorzubeugen.
• Die Graphiken wurden mit dem Computeralgebrasystem MATHEMATICA erzeugt und die generierten POSTSCRIPT-Versionen wurden noch einer programmiertechnischen Verfeinerung unterzogen.
• Übungsaufgaben, die besonders wichtig für das Verständnis des behandelten Stoffs sind und im weiteren verwendet werden, sollten von jeder/m Lernenden bearbeitet werden und sind durch das Symbol gekennzeichnet.
• Besonders schwierige oder technische Übungsaufgaben sind mit einem Stern () gekennzeichnet. Sie sind nur beim Einsatz des Buchs an Hochschulen gedacht.
• Übungsaufgaben, die für Handberechnung zu langwierig erscheinen, tragen das Symbol und sollten mit DERIVE bearbeitet werden. Wir ermuntern ausdrücklich, auch andere Übungsaufgaben - sofern nicht explizit anders gefordert - unter Zuhilfenahme von DERIVE zu lösen. Auch - oder gerade -, wenn die Lösung mit DERIVE nicht immer auf Anhieb gelingen wird, ist der Lerneffekt groß: Bei der Bearbeitung jeder Übungsaufgabe lernt der Schüler oder Student sowohl einen mathematischen Sachverhalt als auch etwas Neues zur Bedienung von DERIVE dazu.
• Englische Übersetzungen wichtiger mathematischer Fachausdrücke sind als Fußnoten angegeben, da Fachliteratur heutzutage meist auch von deutschen Autoren auf Englisch geschrieben wird.
• Gleichungen, auf die verwiesen wird, sind durchnumeriert und rechts mit einer Gleichungsnummer versehen. Tritt eine Gleichungsnummer links auf, so handelt es sich um eine Gleichung, die bereits früher vorkam und zur Erinnerung noch einmal aufgeschrieben wurde.
• Das Ende von Beispielen, Definitionen usw. wird durch das 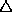-Zeichen angegeben, falls es nicht mit dem Beginn eines neuen Beispiels, einer neuen Definition usw. zusammenfällt. Das Ende eines Beweises ist durch das -Zeichen gekennzeichnet.
• Die Ausgaben von DERIVE sind teilweise versionsabhängig und ebenso von einigen Einstellungen abhängig. In diesem Licht müssen die angegebenen Ausgaben betrachtet werden. Sie können nicht unbedingt genau so reproduziert werden. Ich verwendete grundsätzlich die Standardeinstellung bei der Version 2.54, sofern nicht anders angegeben.
• Gegen Überweisung von 20 DM (Wolfram Koepf, Postbank Berlin, Bankleitzahl 100 100 10, Kontonummer 40 26 21 - 109, Verwendungszweck: DERIVE-Diskette, 360 kB, 1.2 MB oder 3.5 Zoll, mit vollständiger Adresse) kann beim Autor eine Diskette bestellt werden, die alle DERIVE-Sitzungen sowie die mit DERIVE bearbeiteten Übungsaufgaben enthält.