Aufgabe 3.28
Für den freien Fall eines Körpers gilt das Weg-Zeit-Gesetz:
y = -
1 2 9 , 81
x 2 +
v 0 x +
y 0 .
Der Körper wird in der Anfangshöhe
y 0 > 0 mit der
Anfangsgeschwindigkeit
v 0 senkrecht nach oben bzw. nach unten
geworfen.
x bedeutet die Zeit in Sekunden und
y den Abstand
vom Boden in
Metern.
Sei
v 0 = 3 m / s . Welche Anfangshöhe wird benötigt, damit der
Körper die Scheitelhöhe von 60 m erreicht? Welche Anfangshöhe
wird benötigt, damit
der Körper 6 Sekunden in der Luft bleibt?
Sei
y 0 = 55 m . Welche Anfangsgeschindigkeit wird benötigt, damit
der Körper die Scheitelhöhe von 60 m erreicht?
Welche Anfangsgeschindigkeit wird benötigt, damit
der Körper 6 Sekunden in der Luft bleibt?
Der Körper wird in der Anfangshöhe
Sei
Sei
Aufgabe 3.29
Gegeben ist die quadratische Funktion:
y = - 3
x 2 + 5 x - 10 .
Welche Werte auf der
y -Achse werden nicht als Funktionswerte
angenommen und welche Werte kommen als Funktionswerte in Frage?
Geben Sie für jeden Funktionswert
y die Stellen
x an, an
denen dieser Funktionswert angenommen wird!
Welche Werte auf der
Aufgabe 3.30
Von einer Parabel sei der Scheitel
(
x s ;
y s ) = ( - 2 , 3 )
sowie der Punkt
( 5 ; 7 ) bekannt.
Wie lautet die Gleichung der Parabel?
Wie kann man sich die Parabel aus der
Normalparabel entstanden denken?
Aufgabe 3.31
Besitzen folgende quadratischen Funktionen Nullstellen:
y = - 3
x 2 - 2 x + 6 , y = 3
x 2 - 2 x + 6 ?
(Scheitelform herstellen und veranschaulichen).
(Scheitelform herstellen und veranschaulichen).
Aufgabe 3.32
Besitzen folgende Parabeln Schnittpunkte
y = 3 ( x + 2
) 2 + 2 , y = - 2 ( x + 3
) 2 - 4 ,
bzw.
y = ( x + 1
) 2 + 1 , y = 2 ( x - 3
) 2 - 3 ?
(Veranschaulichung durch Zeichnung).
bzw.
(Veranschaulichung durch Zeichnung).
Aufgabe 3.33
Besitzen die folgende Parabel und Gerade Schnittpunkte
y = 2
x 2 - 3 x + 1 , y = 5 x - 4 ?
(Veranschaulichung durch Zeichnung).
(Veranschaulichung durch Zeichnung).
Aufgabe 3.34
Bestimmen Sie nur mit Hilfe von Sätzen aus diesem Modul den Scheitel der Funktion
f ( x ) = - 2
x 2 + 2 x +
5 2 und geben Sie an, ob es sich um einen Hoch- oder Tiefpunkt handelt.
Aufgabe 3.35
Welche der folgenden Punkte liegen auf der Parabel
y = -
1 2 x 2 + 3 x + 5 ?
( 0 , 5 ) , ( - 1 , 10 ) , ( 1 ,
15 2 ) , ( 3 ,
19 2 ) , ( 5 , 5 ) .
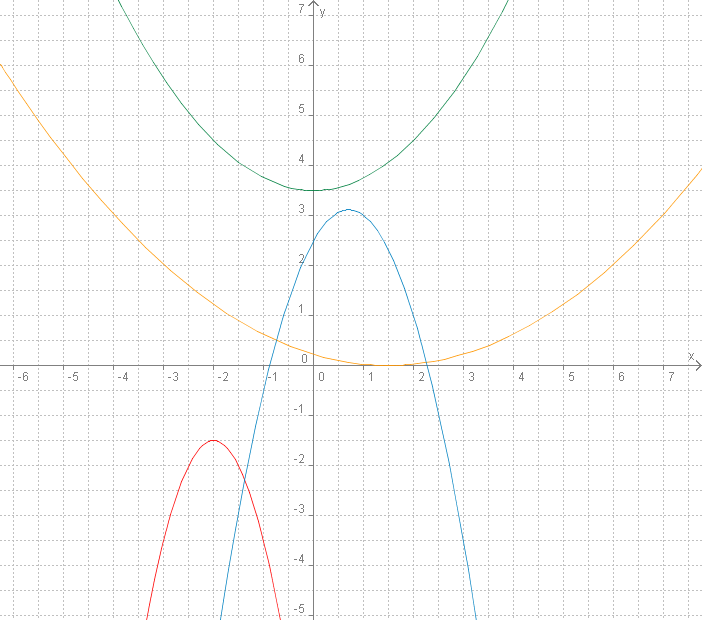
Aufgabe 3.36
Versuchen Sie die Funktionsvorschriften der im unteren Bild dargestellten Parabeln zu bestimmen.