3 Funktionen

Das Beispiel des Ballwurfs hat gezeigt, dass quadratische Funktionen in zwei Aspekten von linearen Funktionen abweichen. Sieht man bei einer linearen Funktion vom Sonderfall der Parallelen zur x-Achse m=0 ab, so werden erstens alle Zahlen auf der y-Achse als Werte angenommen und zweitens besitzen alle diese Werte genau ein Urbild. Beim Ballwurf liegen die Dinge anders. Die Scheitelhöhe kann der Ball nicht überschreiten und gewisse Höhen wurden zu zwei verschiedenen Zeiten durchlaufen. 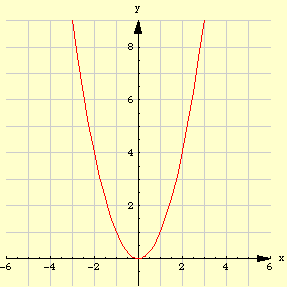Wir betrachten zunächst die Normalparabel, die durch y= x2 gegeben wird. Sie kann keine Funktionswerte annehmen, die negativ sind. Ein Quadrat ist immer größer oder gleich Null. Daraus ergibt sich Null als minimaler Funktionswert der Normalparabel. Dagegen wird jeder y-Wert oberhalb des Minimums tatsächlich als Funktionswert angenommen. Der Wert y=0 wird an der Stelle x=0 angenommen. Geben wir y>0 vor, dann gibt es allerdings zwei Argumente, nämlich
x1 =y    und     x2 =-y
mit
x1 2 =(y )2 =y    und     x2 2 =(-y )2 =y.

Nun gehen wir zur allgemeineren (gestreckten) Parabel über:
y=a x2 .
Im Folgenden sind zwei Fälle zu unterscheiden: (1) a<0 und (2) a>0.

(1) Die Funktionswerte haben einen maximalen Wert und können höchstens den Wert Null erreichen:
a x2 ≤0,
wobei
a x2 =0
gleichbedeutend ist mit:
x= xs =0    und    y= ys =0.
Der Scheitel stellt einen Hochpunkt dar.
(2) Die Funktionswerte haben einen minimalen Wert und können den Wert Null nicht unterschreiten:
a x2 ≥0,
wobei
a x2 =0
wieder gleichbedeutend ist mit:
x= xs =0    und    y= ys =0.
Der Scheitel stellt einen Tiefpunkt dar.

Als Nächstes werden wir den Graphen der Parabel verschieben. Addiert man einen konstanten Wert zum Funktionsterm, so wird die Parabel parallel zur y-Achse verschoben. Beispielsweise wird die um zwei Einheiten nach oben verschobene Normalparabel durch die Funktionsgleichung y= x2 +2, die um drei Einheiten nach unten verschobene Normalparabel durch y= x2 -3 beschrieben. Die Verschiebung parallel zur x-Achse geschieht durch Subtraktion eines konstanten Werts von der Variablen x im Funktionsterm. So wird die um zwei Einheiten nach rechts verschobene Normalparabel durch y=(x-2 )2 , die um vier Einheiten nach links verschobene Normalparabel durch y=(x+4 )2 beschrieben. Natürlich können wir die Parabel auch nacheinander in x- und y-Richtung verschieben. So hat die um drei Einheiten nach unten und um zwei Einheiten nach links verschobene Normalparabel die Funktionsgleichung y=(x+2 )2 -3. Aus dieser Darstellung der Funktionsgleichung lässt sich leicht die Lage des Scheitelpunktes ablesen, der bei (-2,-3) liegt.
Schließen wir den Streckungs- bzw. Stauchungsfaktor a in die Funktionsvorschrift mit ein, gelangen wir schließlich zur Scheitelform:

Wir lösen die Scheitelform der Parabel nach x auf:
y=a(x- xs )2 + ys    ⟺    y- ys a =(x- xs )2    
und demnach:
x1/2 = xs ± y- ys a .
Das Quadrat (x- xs )2 darf nicht negativ werden. Hieraus folgt, dass für a>0 keine Funktionswerte y kleiner als ys , bzw. für a<0 keine Funktionswerte y größer als ys angenommen werden. Für die übrigen Funktionswerte mit Ausnahme von y= ys erhalten wir genau zwei Urbilder.

Die Scheitelform der Parabelgleichung y=a(x- xs )2 + ys multiplizieren wir aus und ordnen nach Potenzen von x:
y = a(x- xs )2 + ys = a( x2 -2 xs x+ xs 2 )+ ys = ax2 -2 xs ax+ axs 2 + ys .
Dies führt auf die allgemeine quadratische Funktionsgleichung der Form:
y= ax2 +bx+c.
Mit einer Gleichung dieser Gestalt wurde der Zusammenhang zwischen der Zeit x und dem Abstand des Balles vom Boden erfasst.

Wenn nichts anderes gesagt wird, soll der Parameter a nicht Null sein: a≠0. Denn für a=0 bekommen wir den Sonderfall der bereits bekannten linearen Funktion.

Wir fragen nun, welche Werte bei quadratischen Funktionen y=a x2 +bx+c angenommen werden können und an welchen Stellen dies geschieht? Hierzu nehmen wir die quadratische Ergänzung zu Hilfe ( a≠0) und schreiben die Gleichung einer quadratischen Funktion in der Scheitelform:
y=a x2 +bx+c=a( x2 +2 b 2a x+ b2 4 a2 )+c- b2 4a =a (x+ b 2a )2 +c- b2 4a .

Die Ergebnisse beim Sonderfall y=a x2 lassen sich unmittelbar übertragen.

Wir haben gesehen: eine Gerade wird durch zwei Punkte festgelegt. In eine Geradengleichung y=mx+b gehen zwei Parameter ein. In die Gleichung einer Parabel y=a x2 +bx+c gehen drei Parameter ein. Man kann sich überlegen, dass drei Punkte eine Parabel festlegen. Die Lösung dieser Aufgabe führt allerdings auf ein System von drei Gleichungen für drei Unbekannte. Übersichtlicher wird das Problem, wenn man die Scheitelgleichung zugrunde legt.

Es gibt einen weiteren wesentlichen Unterschied zwischen linearen und quadratischen Funktionen. Betrachten wir bei einer linearen Funktion y=mx+b die Funktionswerte an der Stelle x und an der Stelle x+Δx. Dem Zuwachs Δx im Argument entspricht der Zuwachs der Funktionswerte:
(m(x+Δx)+b)-(mx+b)=mΔx.
Diese Überlegung bringt noch einmal zum Ausdruck, dass in jedem Steigungsdreieck der selbe Anstieg herrscht. Bei quadratischen Funktionen y=a x2 +bx+c ist das nicht mehr der Fall. Dem Zuwachs Δx im Argument entspricht der Zuwachs der Funktionswerte:
(a(x+Δx )2 +b(x+Δx)+c)-(a x2 +bx+c)=a(2xΔx+(Δx )2 )+bΔx.
Der Zuwachs der Funktionswerte ist nicht unabhängig von der Stelle x, in welcher der Zuwachs im Argument abgetragen wird.